【Programming】Explaining Bitwise Operations

Everyone knows you can perform calculations with numbers using +, -, *, /, but what if I told you that you can also calculate with &, |, ^, ~, <<, >>?
For example, what do you think the results of these are?

12 & 5 =
9 | 6 =
9 ^ 7 =
~10 =
11 << 2 =
7 >> 3 =

Before revealing the answers, I'll explain each operation in detail.
But first, we need to cover the basics of binary numbers.

What is Binary?

Binary is always 0 or 1 and is the counting system computers use to represent all data.
Humans use decimal, handling numbers from 0 to 9.
To bridge the gap between humans and machines, there are two other counting systems: octal and hexadecimal.

What is Octal?

Octal uses numbers from 0 to 7.
It was common in the 1970s and 1980s because processors grouped bits in sets of three.
This was because they were 8-bit processors.
It's still used today, for example, in Unix permissions.

Example: chmod 644 filename.
In binary, 644 translates to 110 100 100.

What is Hexadecimal?

Hexadecimal uses numbers from 0 to F.
It's common in modern computers because 16-, 32-, and 64-bit processors group bits in sets of four.
In binary, 111 is 7, and 1111 is 15, which is F in hexadecimal.
The most well-known use is in HTML or CSS colors.

Example: 0x12120F creates a shade of black used on this website.
In binary, this is 0001 0010 0001 0010 0000 1111.
In decimal, it's 18 18 15.

You might wonder, "Why does hexadecimal 12 equal decimal 18"?
To understand, you need to consider how hexadecimal counts.
Here's a table of numbers:

Hexadecimal	Decimal
00	0
01	1
02	2
03	3
04	4
05	5
06	6
07	7
08	8
09	9
0A	10
0B	11
0C	12
0D	13
0E	14
0F	15
10	16
11	17
12	18

Counting in Binary

To humans, a number like 1100 0110 0001 0010 might seem confusing.
But it's not that difficult.
In decimal, this is 50706.

To understand, you need to see what each bit represents.
Let's start with 4 bits: 0010.
Read from right to left.
The rightmost bit represents 1, the second 2, the third 4, and the leftmost 8.
8, 4, and 1 are false, and only 2 is true.
So, 0 + 0 + 2 + 0 = 2.

Here's a graphic representation:

Upgrading to 8 bits: 0001 0010.
The fifth bit is 16, the sixth is 32, the seventh is 64, and the last is 128.
This is why the Famicom and Game Boy couldn't count beyond 255.
Ignoring the left zeros for 5 bits: 10010.
This is 16 + 0 + 0 + 2 + 0 = 18, which is 18 in decimal and 12 in hexadecimal.

For 12 bits: 0110 0001 0010.
Using the pattern, calculate what each number means:
0 + 1024 + 512 + 0 + 0 + 0 + 0 + 16 + 0 + 0 + 2 + 0 = 1554.
In hexadecimal, 1554 = 612.

Finally, for 16 bits: 1100 0110 0001 0010.
32768 + 16384 + 0 + 0 + 0 + 1024 + 512 + 0 + 0 + 0 + 0 + 16 + 0 + 0 + 2 + 0 = 50706.
In hexadecimal, 50706 = C612.

As a helpful trick, you can count up to 31 using one hand.
Here's how:

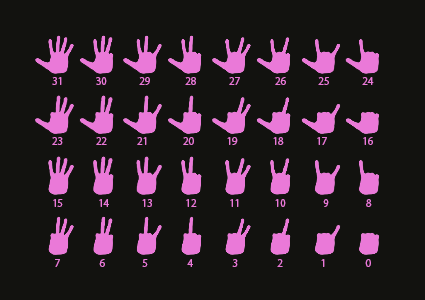
Bitwise Operators

Now that you understand binary basics, let's move on to bitwise operations.
There are six operators:
& (AND), | (OR), ^ (XOR), ~ (NOT), << (Left Shift), >> (Right Shift).

AND Operator

The AND operator compares bits and returns true if both are true.
From the opening question, 12 & 5 = 4.

To understand, let's look at it in binary:

12	5	&
1	0	0
1	1	1
0	0	0
0	1	0

OR Operator

The OR operator compares bits and returns true if either is true.
9 | 6 = 15

9	6
1	0	1
0	1	1
0	1	1
1	0	1

XOR Operator

The XOR operator compares bits and returns false if both are true or both are false.
9 ^ 7 = 14

9	7	^
1	0	1
0	1	1
0	1	1
1	1	0

NOT Operator

The NOT operator inverts all bits.
In other words, 1 becomes 0, and 0 becomes 1.

Warning: Since it inverts the entire byte, using the wrong data type can result in negative numbers.
This is because, in programming languages without types, signed int is used by default.
This is a 32-bit integer with a range of -32,767 to 32,767.
Thus, in PHP, Python, JavaScript, etc., doing ~5 gives -6 instead of the expected result.
In C, since it can't handle integers smaller than 32 bits, this happens:

#include <stdio.h>

int main() {
  int s = 10;
  printf("%d\n", ~s);
  return 0;
}

This results in -11.
This is because C's int is 32 bits (or 16 bits on some systems), so int c = 10; is 0000 0000 0000 0000 0000 0000 0000 1010 in binary, and inverting it results in -11.
To avoid this, you need to add a mask to limit the number of bits to 4:

#include <stdio.h>

int main() {
  int s = 10;
  printf("%d\n", ~s & 0xF);
  return 0;
}

This gives the correct number, 5.

By the way, Zig makes this very easy.
Zig is the only language that natively allows defining a 4-bit unsigned integer.

const std = @import("std");

pub fn main() !void {
  const s: u4 = 10;
  std.debug.print("{d}\n", .{ ~s });
}

This results in 5.
This is because the binary representation of const s: u4 = 10; is 1010.
Using u8, the binary representation is 0000 1010, so ~10 becomes 245 (1111 0101).
Using i8, it becomes -11.

To understand, u8 means "unsigned 8-bit integer", and i8 means "signed 8-bit integer".
The range for unsigned 8-bit is 0 to 255, and for signed 8-bit, it's -127 to 127.
In other words, for unsigned 8-bit, 1111 0101 = -11, but for signed 8-bit, 1111 0101 = 245.

10	~
1	0
0	1
1	0
0	1

Left Shift and Right Shift

Shifting moves bits to the left or right.
However, if bits overflow, they are lost.
11 << 2 = 44
7 >> 3 = 0

To understand, let's look at binary again.
11 = 1011
7 = 0111

For 11 in 8 bits: 11 = 0000 1011.
Shifting 0000 1011 left twice: 0010 1100 = 32 + 8 + 4 = 44.
However, keeping it at 4 bits results in 1100, which is 12.

For 7 >> 3, shifting 0111 right makes all bits 0, resulting in 0.
Extending the bit width to 8, 16, or more bits doesn't matter since bits are counted from the right.
However, 7 >> 1 = 0011 = 3, and 7 << 1 = 1110 = 14.
Since overflowing bits are lost, 7 >> 1 = 0011 = 3, and 3 << 1 = 0110 = 6.

Why Bitwise Operations Exist

In the early days of computers, hardware was very limited, so bitwise operations were a clever way to work around those constraints.
Even today, they're common when handling binary data.
If you're a web developer, you probably don't need to worry about this unless you're building an audio library from scratch in PHP or a packet sniffer in JavaScript.
For low-level software engineers, game programmers (excluding Unity, Unreal, Godot), embedded programmers, or hardware engineers, this knowledge is fundamental.

That's all