【プログラミング】ビット演算の解説

誰もが知っている様に、+、-、*、/ を使って数を計算出来ますが、&、|、^、~、<<、>> でも計算出来ると言ったらどうでしょう？
例えば、以下の結果はどうなると思いますか？

12 & 5 =
9 | 6 =
9 ^ 7 =
~10 =
11 << 2 =
7 >> 3 =

答えを教える前に、全ての操作を詳しく説明します。
その前に、先ず2進数の基本を説明する必要があります。

2進数とは

2進数は常に0又は1で、コンピュータが凡ゆるデータを表現する為に使用する数え方です。
人間は10進数を使い、0から9までの数を扱います。
人間と機械のギャップを埋める為に、2つの他の数え方があります：8進数と16進数。

8進数とは？

8進数は0から7までの数です。
1970年代や1980年代のコンピュータでは、プロセッサが3ビットをグループ化していた為、これが一般的でした。
何故なら、それらは8ビットプロセッサだったからです。/現在でも、Unixの許可等で使われています。

例：chmod 644 ファイル名。
2進数に変換すると、644は110 100 100になります。

16進数とは？

16進数は0からFまでの数です。
16、32、64ビットプロセッサが4ビットをグループ化する為、現代のコンピュータではこれが一般的です。
2進数で111は7、1111は15で、16進数ではFです。
最もよく知られた使用例は、HTMLやCSSの色です。

例：0x12120Fは、このウェブサイトで使用されている黒の色合いを作ります。
2進数では、これは0001 0010 0001 0010 0000 1111に相当します。
10進数では、これは18 18 15です。

「何故16進数の12が10進数の18になるのか？」と疑問に思うかもしん。
その為には、16進数の数え方を考慮する必要があります。
以下は数の表です。

16進数	10進数
00	0
01	1
02	2
03	3
04	4
05	5
06	6
07	7
08	8
09	9
0A	10
0B	11
0C	12
0D	13
0E	14
0F	15
10	16
11	17
12	18

2進数での数え方

人間にとって、1100 0110 0001 0010の様な数は混乱するかもしん。
然し、これはそれ程難しくありません。
10進数では、これは50706です。

これを理解するには、各ビットが何を意味するのかを見る必要があります。
4ビットから始めましょう：0010
右から左に読みます。
右端のビットは1、2番目は2、3番目は4、左端は8を表します。
8、4、1はfalseで、2だけがtrueです。
だって、0 + 0 + 2 + 0 = 2。

ここではそのグラフィック表現を示します：

8ビットにアップグレード：0001 0010
5番目は16、6番目は32、7番目は64、最後のビットは128を表します。
ファミコンやゲームボーイが255を超えて数えられなかった理由はこれです。
左の0を無視して、5ビットにすると：10010
これは16 + 0 + 0 + 2 + 0 = 18で、10進数では18、16進数では12です。

12ビットの場合：0110 0001 0010
これまでのパターンを使って各数が何を意味するのかを理解します。
0 + 1024 + 512 + 0 + 0 + 0 + 0 + 16 + 0 + 0 + 2 + 0 = 1554
16進数では、1554 = 612。

最後に16ビット：1100 0110 0001 0010
32768 + 16384 + 0 + 0 + 0 + 1024 + 512 + 0 + 0 + 0 + 0 + 16 + 0 + 0 + 2 + 0 = 50706
16進数では、50706 = C612。

少し助けになる方法として、片手で31まで数える事が出来ます。
その方法は次の通りです：

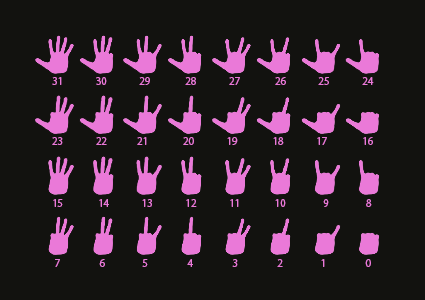
ビット演算子

2進数の基本が分かったので、ビット演算に進みます。
6つの演算子があります：&（AND）、|（OR）、^（XOR）、~（NOT）、<<（左シフト）、>>（右シフト）。

AND演算子

AND演算子はビットを比較し、両方がtrueの場合にtrueになります。
冒頭の質問から、12 & 5 = 4。

これを理解する為に、2進数で見てみましょう：

12	5	&
1	0	0
1	1	1
0	0	0
0	1	0

OR演算子

OR演算子はビットを比較し、どちらかがtrueであればtrueになります。
9 | 6 = 15

9	6	｜
1	0	1
0	1	1
0	1	1
1	0	1

XOR演算子

XOR演算子はビットを比較し、両方がtrue又はfalseの場合にfalseになります。
9 ^ 7 = 14

9	7	^
1	0	1
0	1	1
0	1	1
1	1	0

NOT演算子

NOT演算子は全てのビットを反転させます。
詰り、1は0に、0は1になります。

警告：バイト全体を反転させる為、正しいデータ型を使用しないとマイナスの数になる事があります。
これは、型を持たないプログラミング言語ではデフォルトでsigned intが使用される為です。
これは32ビット整数で、-32,767から32,767の範囲です。
従って、PHP、Python、Javascript等で~5を行うと、期待される結果ではなく-6になります。
C言語では、32ビット未満の整数を扱えない為、これを行うことは出来ません。

#include <stdio.h>

int main() {
  int s = 10;
  printf("%d\n", ~s);
  return 0;
}

これは-11になります。
これは、C言語のintが32ビット（又は一部のシステムでは16ビット）である為、int c = 10;は2進数で0000 0000 0000 0000 0000 0000 0000 1010となり、これを反転させると-11になる為です。
これを回避するには、ビットの数を4に制限するマスクを追加する必要があります：

#include <stdio.h>

int main() {
  int s = 10;
  printf("%d\n", ~s & 0xF);
  return 0;
}

これで正しい数5が得られます。

因みに、Zigではこれが非常に簡単です。
Zigは、4ビットの符号なし整数をネイティブに定義出来る唯一の言語だからです。

const std = @import("std");

pub fn main() !void {
  const s: u4 = 10;
  std.debug.print("{d}\n", .{ ~s });
}

これは5になります。
何故なら、const s: u4 = 10;の2進数表現は1010だからです。
これをu8にすると、2進数表現は0000 1010になり、従って~10は245（1111 0101）になります。
i8にすると-11になります。

これを理解するには、u8は「符号なし8ビット整数」を意味し、i8は「符号付き8ビット整数」を意味します。
符号なし8ビットの範囲は0～255、符号付き8ビットの範囲は-127～127です。
詰り、符号なし8ビットでは1111 0101 = -11、符号付き8ビットでは1111 0101 = 245です。

10	~
1	0
0	1
1	0
0	1

左シフトと右シフト

シフトはビットを左又は右に移動させます。
但し、ビットがオーバーフローすると、ビットを失います。
11 << 2 = 44
7 >> 3 = 0

これを理解するには、再度2進数を見る必要があります。
11 = 1011
7 = 0111

8ビットでの11は11 = 0000 1011。
0000 1011を2回左にシフトすると：0010 1100 = 32 + 8 + 4 = 44。
但し、4ビットのままにすると、結果は1100になり、これは12に相当します。

7 >> 3の場合、0111を右にシフトすると、全てのビットが0になり、結果は0です。
ビット幅を8ビット、16ビット、又はそれ以上に拡張しても、右からビットを数える為、影響はありません。
但し、7 >> 1 = 0011 = 3、そして7 << 1 = 1110 = 14です。
ビットがオーバーフローすると失われる為、7 >> 1 = 0011 = 3、そして3 << 1 = 0110 = 6になります。

ビット演算が存在する理由

コンピュータの初期にはハードウェアが非常に限られていた為、ビット演算はそうした制限を回避する巧妙な方法でした。
然し、今日でも2進数データを扱う際には一般的です。
ウェブ開発者であれば、PHPでオーディオライブラリをゼロから作ったり、Javascriptでパケットスニファーの様なソフトを作ったりしない限り、この記事で説明した内容を気にする必要は殆どないでしょう。
低レベルソフトウェアエンジニア、ゲームプログラマー（Unity、Unreal、Godotを除く）、組み込みプログラマー、又はハードウェアエンジニアにとって、この知識は基本的な物です。

以上